Simplifying Transformer Blocks

Transformer 모델 내부 각 block을 어떻게 단순화시킬 수 있는지에 초점을 맞추고 있습니다. 이때 signal propagation theory와 empirical observations를 통해 설명합니다. 여기서 signal propagation theory는 신호 전파 이론으로 입력 signal이 각 layer를 통과하면서 어떻게 변화하는지를 설명하는 이론입니다. 그런데 이론적 접근만으로 설명하는 것에는 한계가 있어 경험적 관찰을 통해서도 설명합니다. 그리고 이 논문은 Transformer block을 단순화하는 과정에서 학습 속도의 저하 없이 최적화하는 방법에 집중합니다. 이를 위해 고려하는 요소들은 skip connection, projection/value matrices, sequential sub-blocks, 그리고 마지막으로 normalization layers입니다. 결론부터 말씀드리면 이 모든 요소들을 제거할 수 있습니다. 그런데 이것들을 제거하면서 training speed를 희생시키지 않기 위해서 architecture에 약간의 수정을 추가해줍니다.
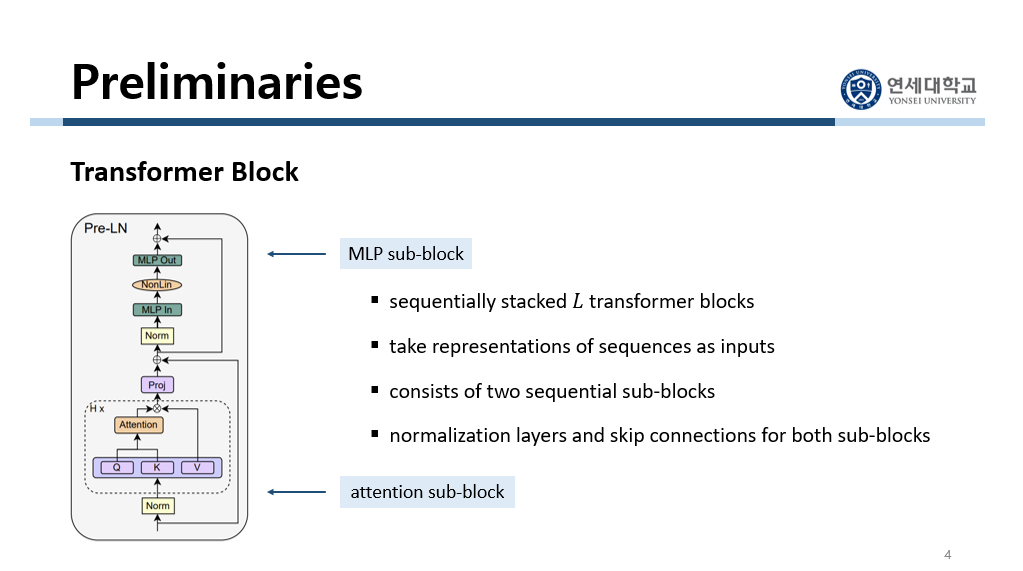
이 논문에서는 기존 Transformer architecture을 이해하는 것이 중요합니다. Transformer 내부는 여러 개의 block이 sequential하게 쌓여 있습니다. 그리고 그 block 내부를 보면 크게 두 개의 sub-block으로 이루어져 있습니다. 하나는 attention sub-block입니다. 여기서는 self-attention mechanism을 통해서 한 token이 다른 token과 어떤 관계를 맺고 있는지 파악합니다. 다른 하나는 Multi-Layer Perceptron인 MLP sub-block입니다. 그리고 각 sub-block 안에서는 normalization layer와 skip connection 단계가 있습니다. Normalization layer에서는 각 출력을 정규화하여 학습 과정을 안정화시킵니다. 그리고 skip connection에서는 입력을 다음 layer의 출력에 직접적으로 더함으로써 깊은 네트워크에서 발생할 수 있는 정보 손실을 방지합니다.
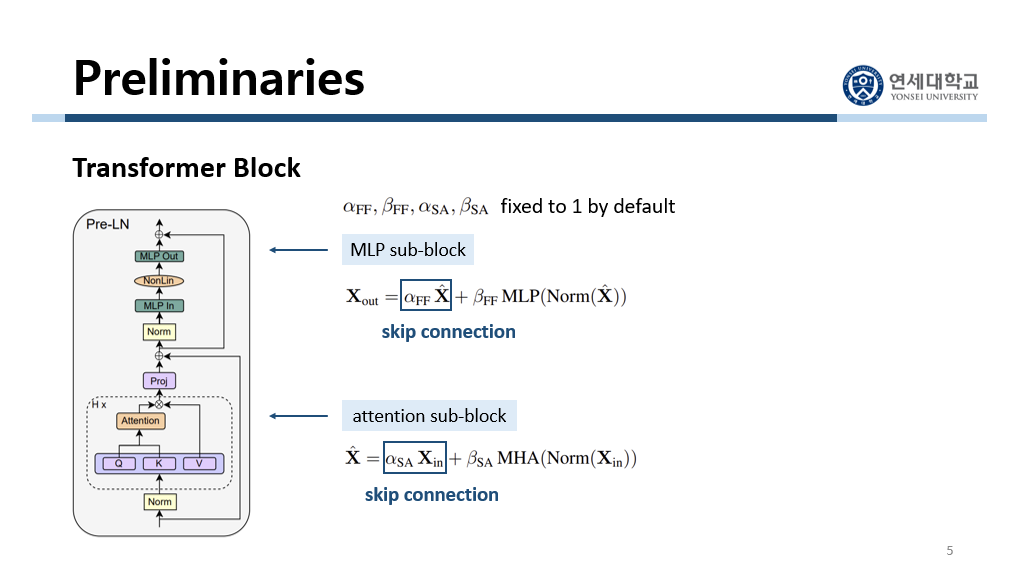
먼저 attention sub-block에서 input이 들어오면 정규화를 시켜줍니다. 그리고 multi-head attention을 거친 결과에 input 값을 그대로 더해줍니다. 이것이 skip connection입니다. Multi-head attention을 거치는 line을 residual branch, 그리고 이 skip connection을 거치는 line을 skip branch라고 합니다. 그리고 이 결과 값이 MLP sub-block으로 들어갑니다. 이 값을 먼저 정규화하고 MLP layer를 거친 후 그 결과에 input 값을 그대로 다시 더해줍니다. 여기서도 skip connection이 적용된 것입니다. 마찬가지로 이 MLP layer를 거치는 line을 residual branch, 그리고 이 skip connection을 거치는 line을 skip branch라고 합니다.
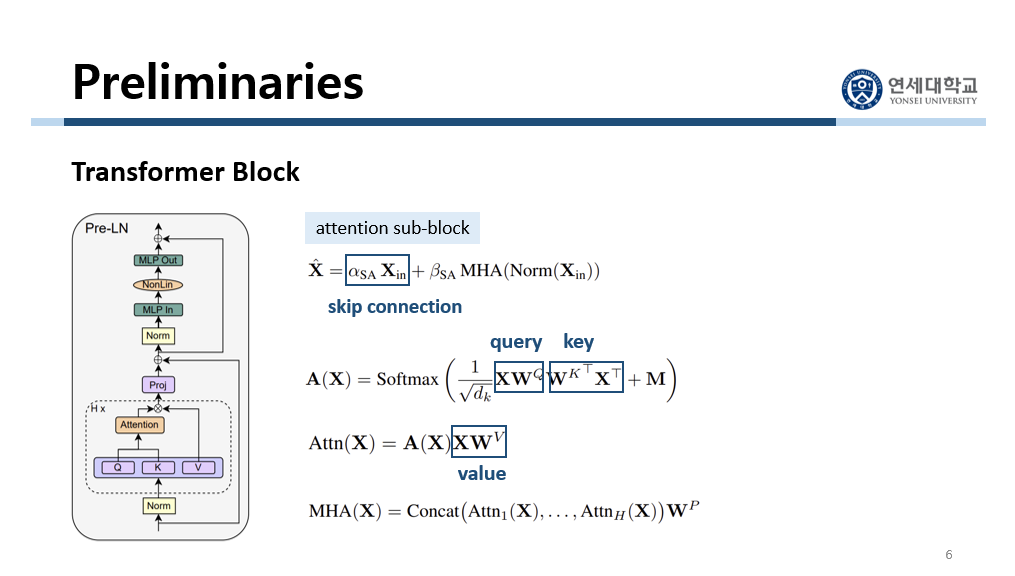
Multi-head attention 과정을 좀 더 자세히 보겠습니다. 여기에 query, key, value 값이 사용됩니다. Query, key, value가 무엇인지는 생략하겠습니다. 먼저 query와 key를 dot product해서 attention score를 구하고 이것을 value에 곱해서 attention value를 구합니다. 이 attention value를 각 head마다 구하는데, 이렇게 각 head마다 구한 attention value를 합하고 projection을 시켜서 multi-head attention value를 구합니다. 이때 이 $W^V$와 $W^P$를 value parameter, projection parameter라고 부릅니다.

이제 각 block을 단순화시키는 과정입니다. 먼저 attention sub-block에서 skip connection을 없애는 시도를 합니다. 그러니까 $\alpha_{SA}$를 0으로 해서 $\alpha_{SA} X_{in}$을 없애는 것입니다. 이때 signal propagation theory에 따르면 단순히 skip connection 부분을 없애면 rank collapse라는 문제가 발생한다고 합니다. 여기서 rank collapse란 skip connection을 없앴을 때 출력 값이 rank가 1인 matrix로 빠르게 수렴한다는 것입니다. Rank가 1인 행렬은 모든 열이나 행이 서로 linear dependent하다는 것으로, 매우 제한적인 정보만을 담고 있습니다. 출력이 rank-1 행렬이 되면 신경망이 다양한 특징을 학습할 때 필요한 표현력을 잃게 됩니다. 출력이 너무 단순화되어서 실제 복잡한 데이터를 효과적으로 처리하기 어렵습니다.

이 문제를 해결하기 위해 architecture를 약간 수정합니다. Attention score를 업데이트할 때 $A(X) \leftarrow (\alpha I_T + \beta A(X) - \gamma C)$로 수정합니다. 이 방법을 shaped attention이라고 합니다. 여기서 $\alpha, \beta, \gamma$는 최적화시켜야 하는 parameter입니다. 그리고 $C$는 학습시키지 않는 그냥 constant입니다. 이 값은 query-key dot product가 0일 때 attention score $A(X)$ 값으로 고정시켜 놓습니다. 그래서 query-key dot product가 0일 때는 attention score $A(X)$와 $C$가 같습니다. 이때 beta와 gamma가 같으면 $\beta A(X) - \gamma C$가 0이 되어 날라갑니다.

Rank collapse라는 문제점을 해결하기 위해 attention score를 업데이트할 때 몇 가지 수정을 합니다. 먼저 초기화 단계에서 query parameter인 $W^Q$를 0으로 하고 $\alpha, \beta, \gamma$를 모두 1로 합니다. 초기 단계에서 query parameter를 0으로 했기 때문에 query key dot-product는 0이 됩니다. 그래서 현재 attention score $A(X)$와 $C$는 값이 같습니다. 이때 $\beta$와 $\gamma$가 같게 설정했기 때문에 $\beta A(X) - \gamma C$가 0이 되어 날라가게 됩니다. 그리고 $\alpha$는 1로 초기화하였기 때문에 초기화 단계에서 attention score는 그냥 identity matrix가 됩니다. 이것은 signal propagation theory에 따르면 좋은 signal propagation이라고 합니다. Self-attention matrix를 identity matrix로 초기화시키면 학습 초반에 다른 토큰보다 자기 자신 토큰에 집중하게 됩니다. 모델의 초기 학습 단계에서는 parameter가 아직 최적화되지 않은 불안정한 상태입니다. 이때 토큰이 자기 자신에게 더 집중하도록 하면 안정성을 증진시킬 수 있습니다. 그리고 추가적으로 성능 향상을 위해서 각 head마다 다른 $\alpha, \beta, \gamma$ parameter를 설정합니다. 그리고 마지막으로 MLP branch 효과를 낮춰줍니다. Skip connection을 하는 이유는 residual branch 부분의 효과를 낮추기 위해서입니다. 그런데 지금 skip connection을 없앴기 때문에 residual branch 부분의 효과가 너무 셉니다. Signal propagation theory에 따르면 MLP sub-block에서든 attention sub-block에서든 skip connection을 없애면 residual branch 부분의 효과가 상대적으로 강해집니다. 그래서 이 효과를 줄여줘야 합니다. 즉 $\beta_{FF}$가 $\alpha_{FF}$보다 작은 값을 갖도록 합니다.

이렇게 skip connection을 없앴고, 없앰으로써 rank collapse 문제를 발생시키지 않기 위해 attention score를 업데이트할 때 수정을 추가했습니다. 그런데 attention score 업데이트하는 과정을 보면 원래보다 최적화해야 하는 parameter 개수가 늘어났습니다. 게다가 head마다 다른 $\alpha, \beta, \gamma$ 값을 쓴다고 해서 parameter 개수가 훨씬 많아졌습니다. 그래서 지금 부작용으로 training speed가 매우 높아졌습니다. 그래프를 보시면 초록색 선이 skipless network이고 보라색 선이 skip connection이 있는 network입니다. 이 그래프의 y축은 training speed에 대한 loss인데 초록색 선인 skipless network에서 loss가 더 높습니다. 그러니까 skip connection을 없앴더니 학습 시간이 길어졌다는 것입니다. 이 부작용을 해결하기 위해서 value parameter와 projection parameter를 수정했습니다. $W^V$와 $W^P$는 최종 가중치입니다. 그리고 $W_{init}^V$와 $W_{init}^P$는 초기 가중치입니다. 초기 가중치에서 $\Delta W^V$와 $\Delta W^P$만큼의 변화량이 생겨서 최종 가중치가 형성된 것입니다. 이때 signal propagation theory에 따르면 $W^V$와 $W^P$의 초기값을 orthogonal matrix로 하면 수렴 속도를 높일 수 있다고 합니다. 그래서 저자들은 orthogonal matrix 중 identity matrix를 선택합니다. 즉 $W^V$와 $W^P$의 초기값을 identity matrix로 하여 수렴 속도를 높인 것입니다.
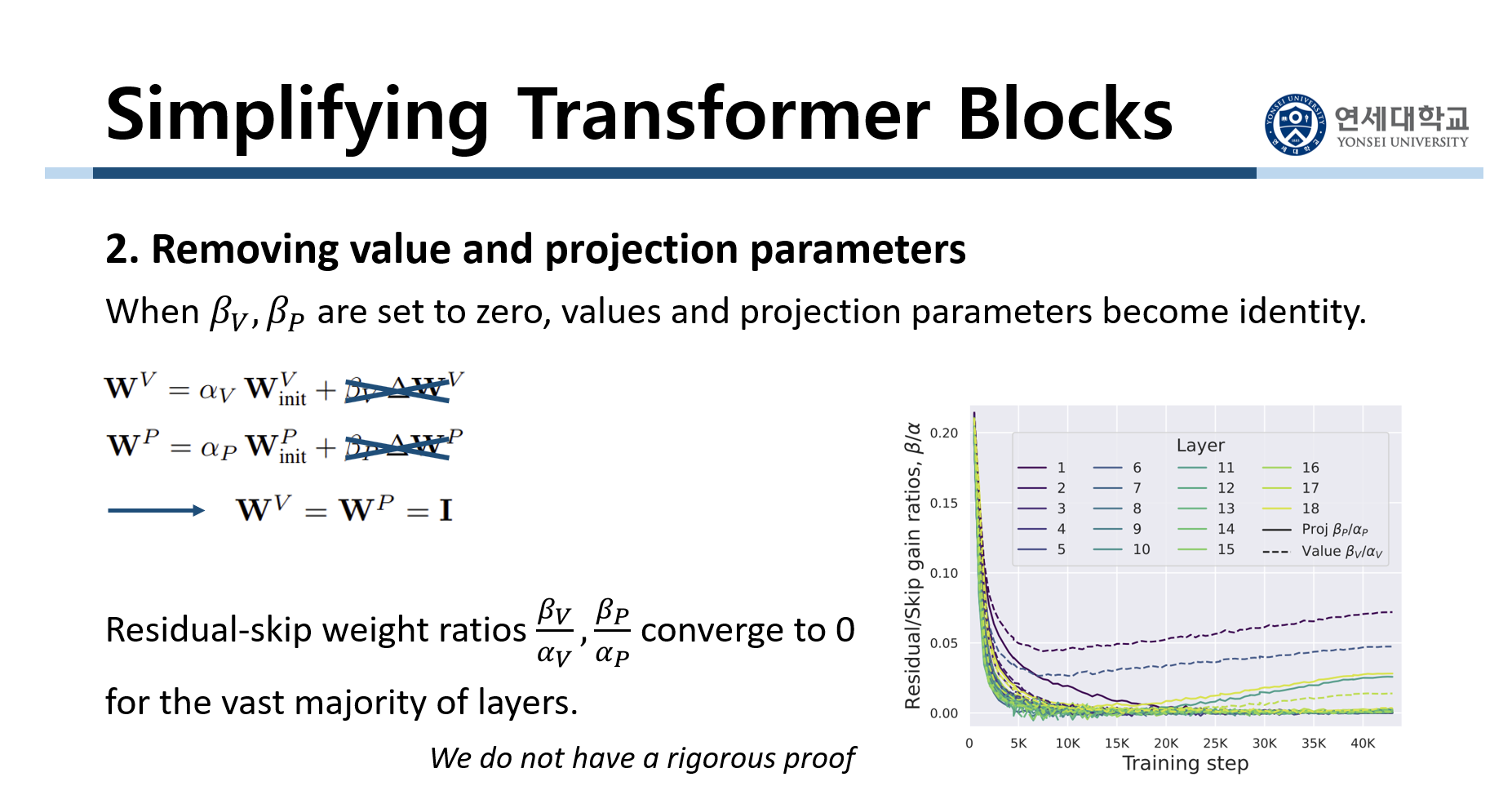
다음으로 value parameter와 projection parameter를 없앴습니다. 직전에 value parameter와 projection parameter를 reparameterization했습니다. 그리고 $W^V$와 $W^P$의 초기값을 identity matrix로 설정했었습니다. 그런데 여기서 $\beta_V$와 $\beta_P$를 0으로 해서 $\beta_V \Delta W^t$와 $\beta_P \Delta W^P$을 아예 없애버립니다. 그러니까 $W^V$와 $V^P$는 매번 업데이트가 되지 않고 항상 identity matrix로 유지되는 것입니다. 그래프는 training에 따른 $\alpha$와 $\beta$의 비를 나타냈습니다. 대부분의 layer에서 training이 지속될수록 이 비가 0으로 수렴하는 것을 경험적으로 확인할 수 있었습니다. 그러니까 $\beta$들은 매우 작은 값이 되고 $\alpha$들은 매우 큰 값들이 되는 것입니다. 그래서 어차피 training이 진행되면서 $\beta$가 매우 작은 값이 되기 때문에 그냥 처음부터 $\beta$를 0으로 고정시킵니다. 그리고 여기에 대해서 논문 저자들은 we do not have a rigorous proof라며 그저 경험적으로 이렇게 할 수 있음을 보였습니다.
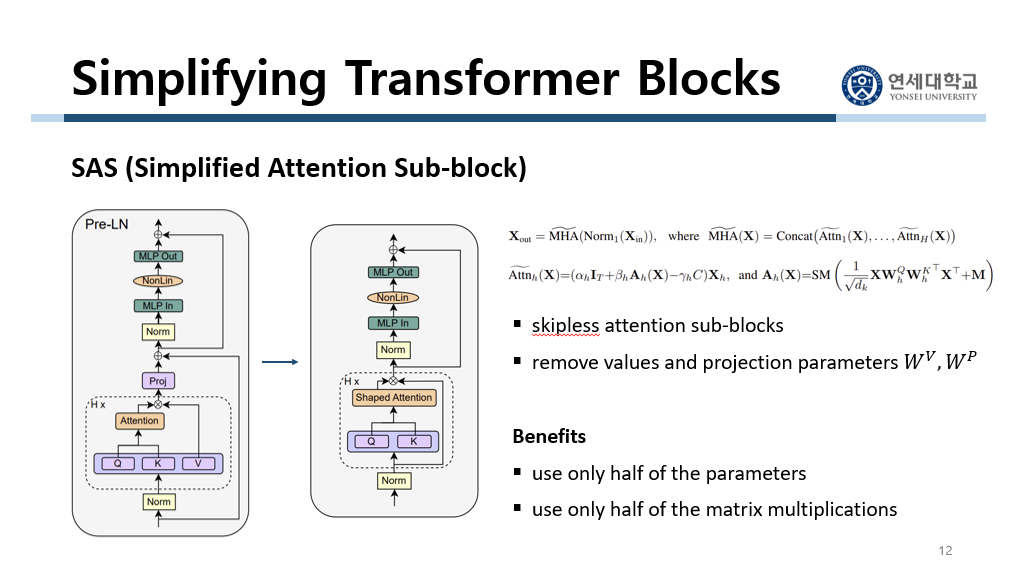
지금까지의 수정 사항을 정리하겠습니다. 먼저 attention sub-block에서 skip connection을 없앴습니다. 이때 shaped attention을 사용했습니다. 그림을 보면 skip branch가 사라졌습니다. 그리고 $W^V$와 $W^P$를 identity matrix로 해서 수식에 $W^V$와 $W^P$가 사라졌습니다. 그래서 그림에서 value가 없어졌고, 여러 개의 head를 거쳐서 합친 후에 하는 projection이 사라졌습니다. 이 구조를 Simplified Attention Sub-block이라고 해서 SAS라고 칭합니다. 이 구조의 benefit은 value parameter와 projection parameter를 업데이트하지 않아도 되기 때문에 parameter가 줄어들었다는 것입니다. 그리고 행렬 곱 계산이 줄어들었습니다. 이제 여기서 이 구조를 더 단순화시킵니다.

아까는 attention sub-block에서 skip connection을 제거했습니다. 이번에는 MLP sub-block에서 skip connection을 제거합니다. 즉 activation을 상대적으로 더 linear하게 하는 것입니다. 그런데 아까와 마찬가지로 여기에서도 학습 시간이 길어지는 부작용이 발생했습니다. 그래프를 보시면 MLP sub-block에서 skip connection을 없앤 경우 training speed에 대한 loss가 큰 것을 확인할 수 있습니다. 이를 해결하기 위해서 parallel한 구조를 사용하는 idea를 냅니다. 이것은 multi-head attention sub-block과 MLP sub-block을 parallel하게 위치시키는 것입니다. 원래 MHA에서 나온 값이 MLP에 입력으로 들어갔는데 지금은 parallel하게 위치되어 있습니다. 이것에 대한 근거는 sequential 구조보다 parallel 구조가 training speed 측면에서 15% 빠르다는 선행 연구 결과가 있기 때문입니다.

이렇게 parallel한 구조를 사용하면 MLP sub-block에서 skip connection을 없앴을 때 학습 속도가 느려지는 것을 방지할 수 있습니다. 그래서 parallel한 구조를 적용하면서 MLP sub-block에서 skip connection을 없앱니다. 이 구조를 SAS-Parallel이라 하고, 줄여서 SAS-P라고 합니다. 이 구조는 아까 SAS 구조에서 더 단순화시킨 구조입니다. 그래서 multi-head attention sub-block과 MLP sub-block, 모든 sub-block에서 skip connection을 없앤 것입니다. 그리고 마찬가지로 skip connection을 없애서 세진 MLP branch 효과를 낮춰줬습니다. 즉 $\beta_{FF}$ 값을 줄인 것입니다.
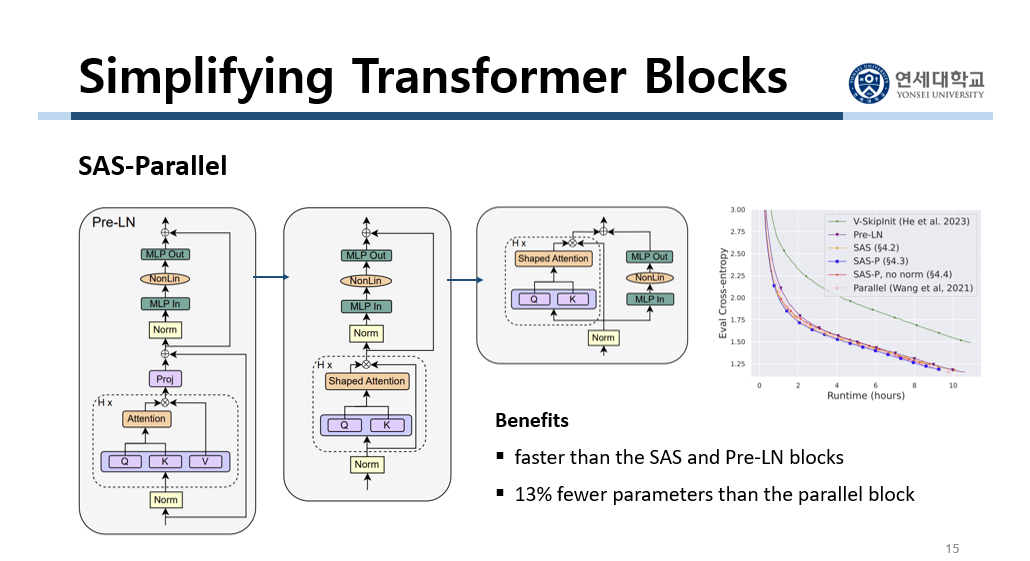
세 번째 그림이 SAS-P 구조입니다. 여기서는 SAS와 달리 MLP sub-block에서 skip connection이 없어졌고, MLP sub-block과 multi-head attention sub-block이 parallel하게 위치해 있습니다. 이렇게 함으로써 얻는 benefit은 SAS랑 기존의 구조보다 training 속도가 빠르다는 것입니다. 그래프를 보면 SAS-P가 SAS나 Pre-LN보다 training speed에 대한 loss가 작습니다. 그리고 처음으로 parallel 구조를 제안한 선형 연구의 모델이 분홍색 선입니다. 이 모델과 학습 속도가 비슷합니다. 그런데 SAS-P는 이 모델보다 13% 더 적은 parameter를 가지고 있습니다. SAS-P는 비슷한 학습 속도를 가지고 있으면서 parameter 개수가 더 적은 것입니다.

마지막으로 normalization layer를 없앴습니다. Normalization layer의 효과는 skip connection과 마찬가지로 residual branch의 효과를 줄여주는 것입니다. 그런데 normalization layer를 없애면 이 효과를 줄여주지 못합니다. 그래서 강제로 residual branch 효과를 낮춰줘야 합니다. 그 방법으로는 attention matrix를 identity matrix와 비슷하게 하는 것, 그리고 MLP 구조를 상대적으로 더 linear하게 바꾸는 것입니다. 그런데 이 조건들은 이미 앞에서 구조를 수정하면서 이미 충족되었습니다. Shaped attention을 사용해서 identity matrix와 비슷하게 했고, MLP sub-block에서 상대적으로 비선형성을 증가시키는 skip connection을 없앴습니다. 따라서 이번에는 구조 수정 없이 그냥 normalization layer만 제거해주면 됩니다. 이렇게 해도 된다는 증거가 밑의 그래프입니다. 이 그래프는 normalization layer를 없앴는데도 training speed 희생이 없었다는 것을 보여줍니다. 이것 또한 경험적으로 확인한 것입니다. 그래프를 보면 SAS-P에 normalization layer를 없앤 것이 빨간색 선입니다. Normalization layer를 없앴는데도 학습 속도가 크게 늘어나지 않았습니다.
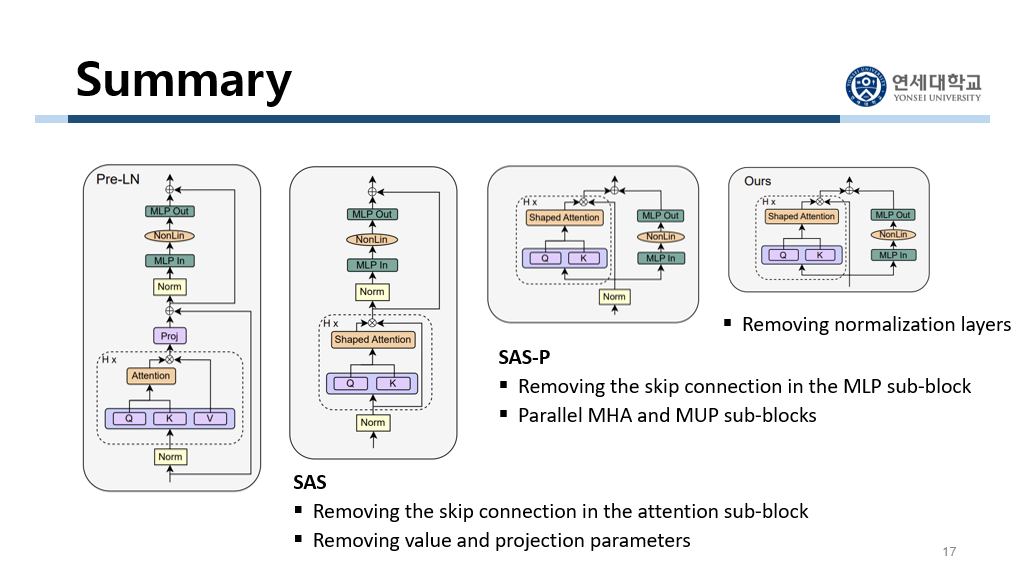
가장 왼쪽의 그림이 기존의 Transformer block입니다. 여기서 attention sub-block에서 skip connection을 없앴습니다. 그리고 value와 projection parameter를 없앴습니다. 이것을 SAS라고 합니다. 그리고 MLP sub-block에서 skip connection을 없앴습니다. 그리고 늘어난 학습 속도를 줄이기 위해서 parallel한 구조를 채택했습니다. 이것을 SAS-P라고 합니다. 그리고 마지막으로 SAS-P에서 normalization layer를 없앴습니다. 이게 이 논문에서 제안한 단순화된 모델의 최종 architecture입니다.
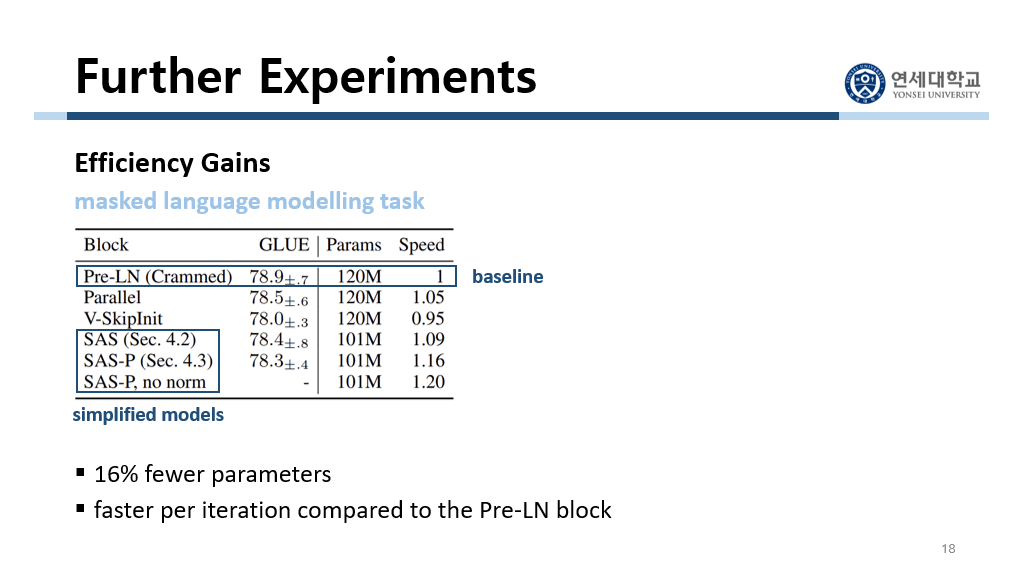
이 구조로도 NLP task를 잘 수행할 수 있음을 나타내기 위해서 실험을 진행했습니다. 이때 downstream task로 masked language modelling task를 수행하게 했습니다. 먼저 baseline은 기존의 Transformer 구조인 Pre-LN입니다. 그리고 두 번째의 parallel은 처음으로 parallel 구조를 제안한 논문의 모델입니다. 그리고 마지막 세 개의 모델은 이 논문에서 제안한 모델들입니다. 이 논문에서 제안한 모델들은 16% 더 적은 parameter를 가지고 있습니다. 그럼에도 불구하고 speed는 baseline보다 더 빠릅니다. 즉 이 논문에서 제안한 모델들은 효율적이라고 할 수 있습니다.
paper