Gamma Poisson Shrinker
Gamma Poisson Shrinker는 베이지안 방법을 적용하여 실마리 정보를 탐지한다.
-
시판 후 안전성 검사 (Post-market Safety Surveillance): 의약품이 시장에 출시된 후에 계속해서 그 안전성과 효과를 감시하는 과정
-
이상 사례 (Adverse Effect) : 의약품 투여하거나 사용하는 도중 발생한 바람직하지 않고 의도되지 않은 징후, 증상 또는 질병
-
실마리 정보 (Signal): 약물과 이상 사례 간의 새로운 잠재적 인과관계를 제시하는 정보
-
실마리 정보 탐지 (Signal Detection): 시판 후 안전성 검사에서 실마리 정보를 탐지하는 과정
기본 원리
의약품과 이상 사례 쌍을 만든다. 각 쌍마다 실제 보고 건수와 기대되는 보고 건수를 구한다. 그리고 실제 보고 건수와 기대되는 보고 건수를 비교한다. 기대되는 보고 건수보다 실제 보고 건수가 월등히 높을 때 실마리 정보라고 탐지한다.
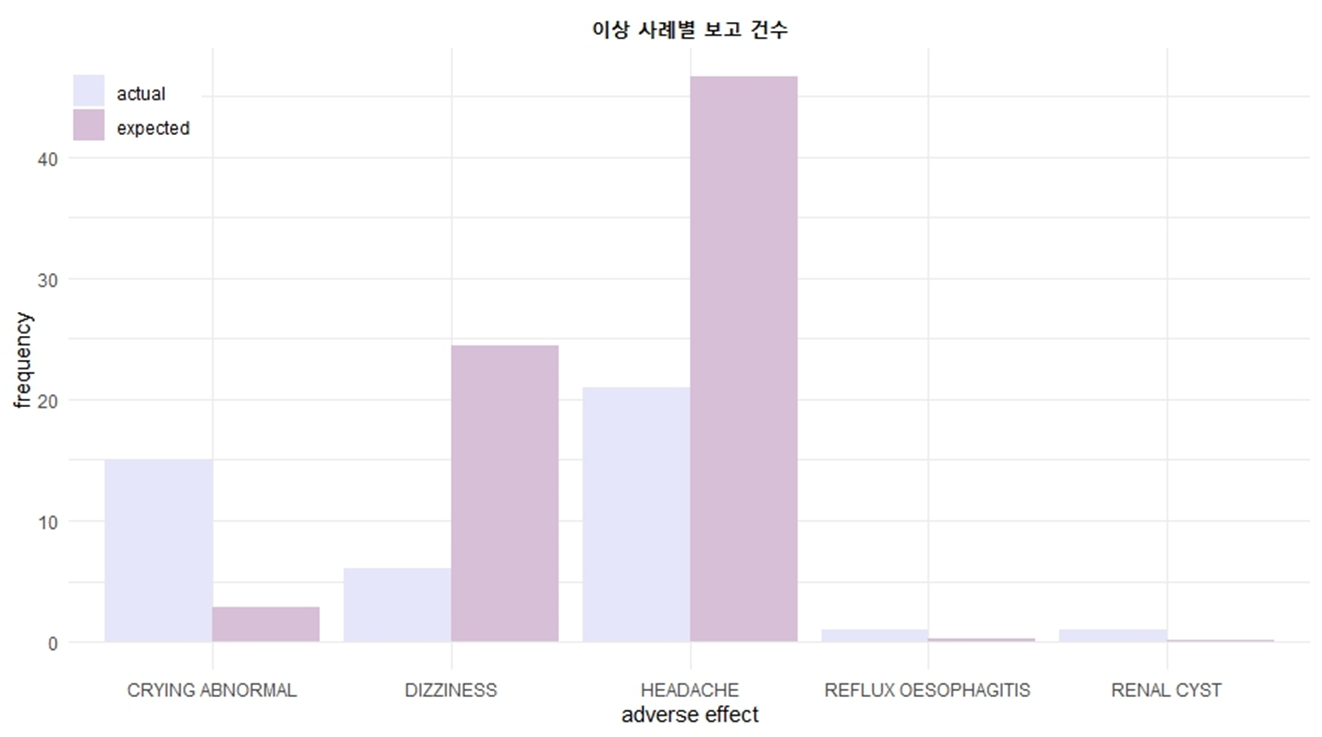
위 그래프는 meningococcus A,C,Y,W-135, tetravalent purified polysaccharides antigen conjugated라는 약물 투여 중 발견된 이상 사례 5개를 나타냈다. 이때 CRYING ABNORMAL이라는 이상 사례가 기대되는 보고 건수에 비해 월등히 높다. 이러한 경우 실마리 정보라고 탐지될 것이다.
Notation
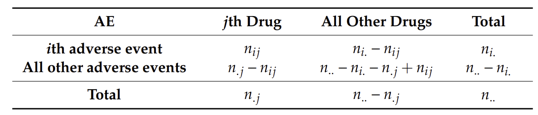
Relative Report Rate
실제 보고 건수와 기대되는 보고 건수의 비율이고 $\lambda_{ij}$라 한다. 기대되는 보고 건수를 계산할 때 의약품과 이상 사례의 독립성을 가정한다.
\[\lambda_{ij} = \frac{n_{ij}}{E_{ij}} \quad where \ \ E_{ij} = \frac{n_{i.} \times n_{.j}}{n_{..}}\]
가설 설정
귀무가설을 실제 보고 건수와 기대되는 보고 건수가 같다고 설정한다.
$H_0: \lambda_{ij} = 1$
$H_a: \lambda_{ij} > 1$
Model
개수에 대한 데이터이기 때문에 포아송 분포를 설정한다.
\[n_{ij} | \lambda_{ij} \ \sim^{iid} \ Poisson(\mu_{ij}) \quad where \ \ \mu_{ij} = E_{ij} \times \lambda_{ij}\]
사전 분포 (Prior Distribution)
사전 분포는 혼합 감마 분포로 설정한다. 이때 hyperparameter는 empirical Bayes method로 정한다. 즉 $\alpha_1, \beta_1, \alpha_2, \beta_2, w$는 $n_{ij}$의 marginal distribution의 likelihood를 최대화하는 것으로 정한다. $n_{ij}$의 marginal distribution의 likelihood는 혼합 negative binomial 분포로 나온다.
\[\lambda_{ij} \ \sim \ w \times Gamma(\alpha_1, \beta_1) + (1 - w) \times Gamma(\alpha_2, \beta_2)\]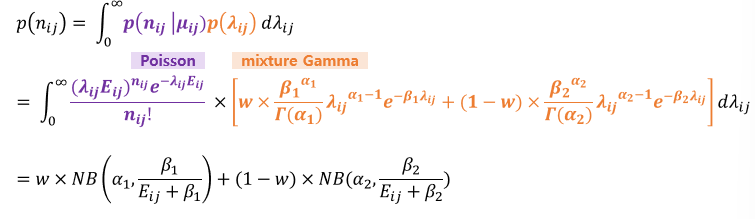
이렇게 hyperparameter를 구하게 되면 데이터의 분포와 비슷한 사전 분포가 만들어진다.
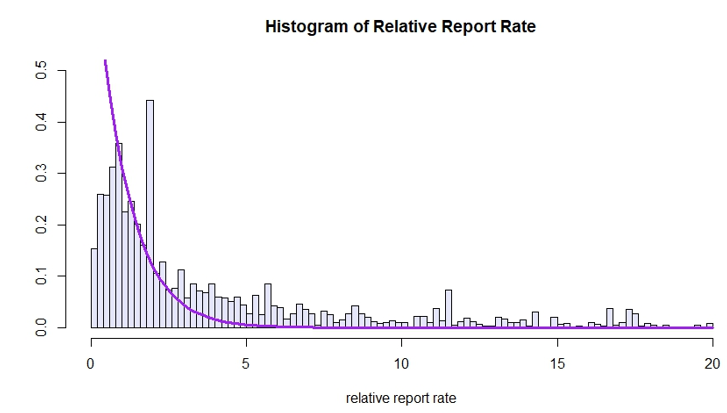
위 그래프는 relative report rate의 히스토그램에 empirical Bayes method로 구한 사전 분포를 그 위에 나타낸 것이다. 데이터와 비슷하게 사전 분포를 잘 구했음을 알 수 있다.
사후 분포 (Posterior Distribution)
감마 분포가 포아송 분포의 conjugate prior이므로 사후 분포는 혼합 감마 분포로 나온다.

실마리 정보 탐지
사후 분포에서 $\lambda_{ij}$의 EBGM을 구한다. 이 EBGM 값이 2보다 크면 실마리 정보로 감지하게 된다. 이는 관찰된 사건 발생률이 예상치의 두 배라는 것으로, 경험적으로 통용되는 실마리 정보 탐지 기준이다. EBGM은 empirical Bayesian geometric mean으로 기하 평균을 구하면 되는 것이다.
R 패키지: openEBGM
이 패키지는 사전 분포의 hyperparamter를 설정하는 함수, 성별이나 연령과 같은 변수를 고려하기 위해 stratification하는 기능, EBGM에 대한 credible interval을 구하는 함수 등을 포함한다.