Self-Polish: Enhance Reasoning in Large Language Models via Problem Refinement
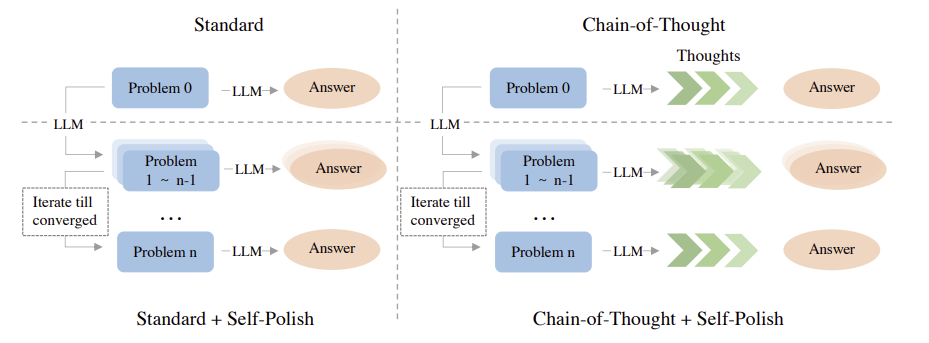
Chain-of-Thought(CoT)는 LLM의 추론 능력을 향상시키기 위해 모델이 근거와 답변을 생성하는 중간 추론 과정에 집중한다. 하지만 Self-Polish는 모델에게 제시한 문제를 더 이해하기 쉽고 해결 가능하도록 세밀하게 다듬는 것에 초점을 둔다. 이 Self-Polish 방법은 다른 prompting 기법들과 서로 영향을 주지 않는 독립적인 관계에 있기 때문에 다른 prompting 기법들과 함께 사용하여 추가적인 개선을 이룰 수 있다.
Problem Refining Priniciples

(1) Conciseness: 문제들은 이해하기 쉽도록 하기 위해 너무 길지 않아야 한다.
(2) Clarity: 문제들은 모호한 표현을 피해야 한다.
(3) Focus: 문제들은 의도한 바를 명확하고 분명하게 밝히고 있어야 한다.
(4) Absence of Irrelevant Information: 문제들은 모델에게 혼란을 줄 수 있는 불필요한 정보가 없어야 한다.
Zero-Shot Problem Refining
예제들을 구축하기 어렵고 모델이 새로운 데이터를 학습할 때 이전에 학습했던 정보를 잊어버리는 현상인 forgetting problems가 있기 때문에 훈련 없이 앞선 원칙들을 내재화시킨다. 먼저 모델에게 instruction을 준다. Prompt에는 [Instruction, 원래 문제]가 들어간다. 그러면 모델은 새롭게 생성된 문제를 제시하고 이 문제를 사용하여 답변을 낸다. 답변을 낼 때에는 standard 방법, CoT 방법, LtM 방법 등 어떠한 방법을 사용해도 된다.
In-Context Problem Refining
Zero-Shot은 어쩔 수 없이 성능 향상에 제한이 있다. 따라서 몇 가지 예제를 추가하는 방법도 있다. 이때에는 [원래 문제, 새로운 문제]로 이루어진 몇 가지 예제를 모델에게 제시하며 여러 가지 refining pattern을 소개한다. 예를 들어 관련 없는 정보를 제거하거나 여러 문장을 새로운 문장으로 요약하거나 논리 구조를 재배열하는 것이 있다. 이렇게 생성된 새로운 문제로 최종 답을 얻는다. In-Context Problem Refining은 Zero-Shot Problem Refining보다 더 큰 성능 향상을 보였다.
Progressively Refining
Refining한 문제의 일관성을 위해서 Progressively Refining 방법을 제시한다. 문제에 대한 답변을 제시하고 문제를 refining하는 것을 조건을 충족시킬 때까지 번갈아 실행한다. 반복을 멈추게 하기 위해서는 두 가지 조건이 있다. 먼저 첫 번째는 마지막 두 답변이 일관된 경우이다. 이때에는 답변이 수렴했다고 판단하여 반복을 멈춘다. 위의 그림에서는 마지막 두 답변이 같으므로 수렴했다고 판단한 것이다. 다른 하나는 최대 반복 횟수 K = 3을 초과하는 경우이다. 밑의 표를 보면 반복을 많이 할수록 수렴하는 경향을 보인다.
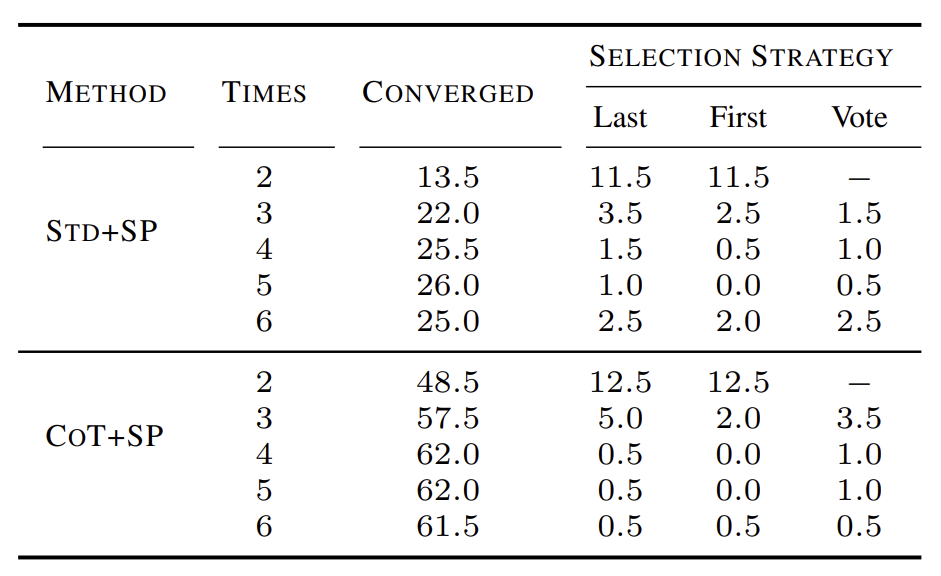
Results
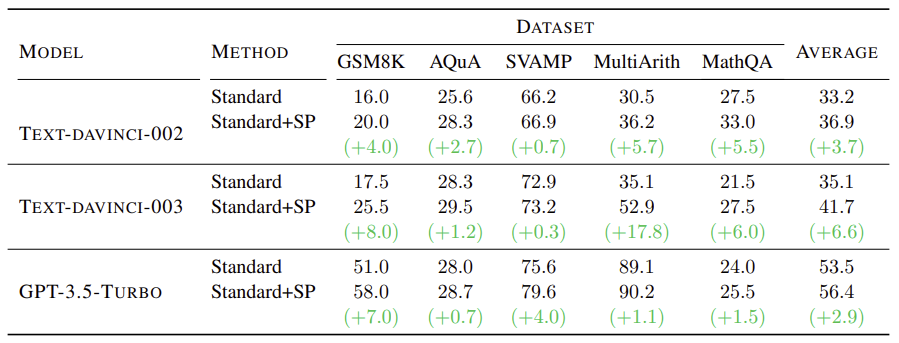
위 표는 standard few-shot prompting 기법에 Self-Polish 기법을 추가한 결과를 나타낸다. 모든 데이터셋에 대해서 성능 향상을 보인다. 특히 text-davinci-003 모델에 Self-Polish 기법을 사용했을 때 MultiArith 데이터셋에서 매우 큰 성능 향상을 보였다. GPT-3.5-turbo 모델에 Self-Polish 기법을 사용했을 때에는 성능 향상이 크지 않다. 이는 GPT-3.5-turbo 모델이 이미 문제를 해석하는 능력이 뛰어나기 때문이다.
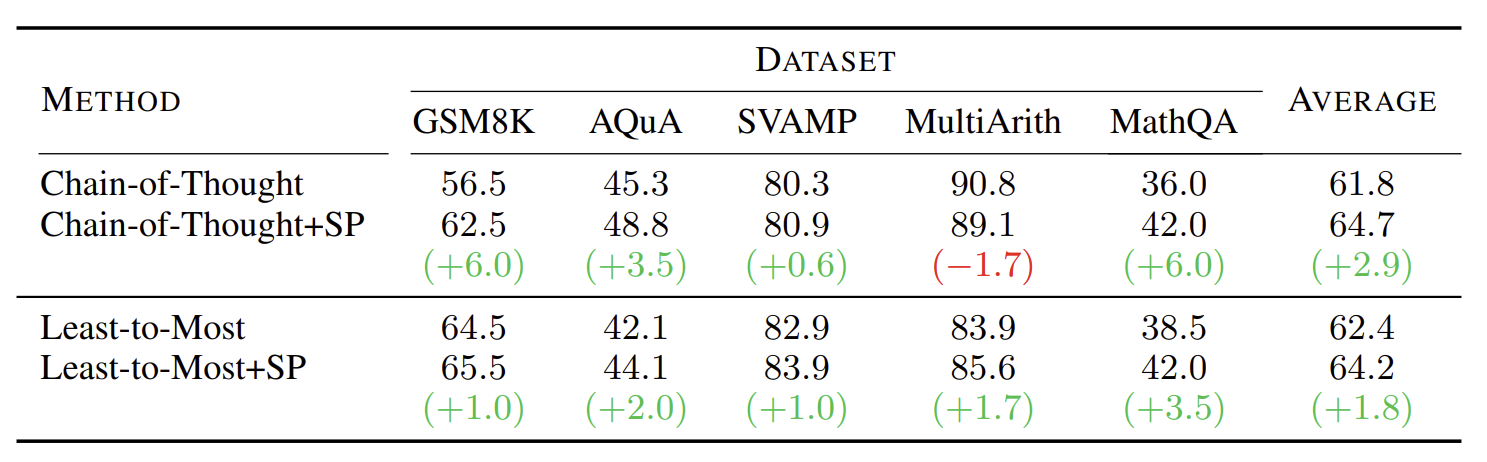
위 표는 standard few-shot prompting 기법 뿐만 아니라 다른 기법에 Self-Polish 기법을 추가했을 때 결과를 나타낸다. CoT와 LtM 기법에 Self-Polish 기법을 함께 사용했더니 성능이 향상되었다. LtM보다는 CoT 기법과 사용했을 때 성능 향상이 더 크다. 이는 LtM은 문제를 분해하면서 Self-Polish 기법의 효과가 저절로 나타났기 때문이다. 그리고 어려운 task에 사용할수록 성능 향상이 크다. 즉 Self-Polish 기법은 복잡한 추론 문제에 효과적인 기법이다.
paper