Selective Mixup Helps with Distribution Shifts, But Not (Only) because of Mixup

Selective Mixup

훈련 데이터의 샘플을 혼합하여 새로운 샘플을 생성하는 방법을 mixup이라고 한다. 훈련 데이터와 테스트 데이터 사이에 class 비율이 다르면 모델은 훈련 데이터에서 더 많이 나타나는 class를 선호하게 되어 실제 환경에서 성능이 저하된다. 이에 대한 해결책으로 class 간 mixup을 한다. 즉 두 class의 데이터를 선형적으로 결합하여 새로운 학습 샘플을 생성한다. 만약 $x_1$의 class는 A, $x_2$의 class는 B라고 할 때 원-핫 인코딩으로 표현하면 A의 class는 $[1, 0]$, B의 class는 $[0, 1]$이 된다. $x_1$과 $x_2$를 선형적으로 결합한 새로운 학습 샘플 $x$는 $x = \lambda x_1 + (1 - \lambda) x_2$로 만들어진다. 이때 새로운 $x$의 class는 class A와 class B의 속성을 일정 비율로 혼합했기 때문에 $[\lambda, 1 - \lambda]$가 된다.

그림1.png

그리고 selective mixup이란 데이터의 샘플을 혼합하는 과정이 특정 기준이나 조건에 따라 선택적으로 이루어지는 것이다. 예시로 서로 다른 class 간의 데이터 만을 조합하는 것은 selective mixup이다. 본 논문은 selective mixup이 훈련 데이터와 테스트 데이터 간의 분포 차이에 대응하는 데 도움을 주지만 그 이유가 단순히 mixup 때문이 아니라고 주장한다. 즉 mixup 자체보다는 어떤 예시를 어떻게 조합하느냐가 모델의 일반화 성능에 중요한 역할을 한다고 설명한다.

Background: Mixup and Selective Mixup

모델 $f_\theta : \mathbb{R}^d \rightarrow [0, 1]^C$: 학습된 매개변수 $\theta$를 가진 분류 모델
- 입력: $d$-차원의 입력 벡터 $x$
- 출력: $C$개의 class에 대한 벡터 $y$
훈련 데이터: $\mathcal{D} = {(x_i, y_i, d_i)}_{i = 1}^n$
- $y_i$: 원-핫 인코딩된 ground-truth 레이블
- $d_i$: 도메인 인덱스 (이미지 스타일, 시간대 등)
Training with ERM: $\mathcal{R} (f_\theta, \mathcal{D}) = \mathbb{E}{(x, y) \in \mathcal{D}} \ \mathcal{L} (f\theta (x), y)$를 최소화하는 매개변수를 찾음
- 손실 함수 $\mathcal{L} (f_\theta (x), y)$: 모델의 예측과 실제 레이블 사이의 오차 측정
- 데이터셋에 있는 모든 샘플에 대한 손실 함수에 산술 평균을 취함
Training with mixup: 무작위로 뽑힌 두 데이터를 혼합함
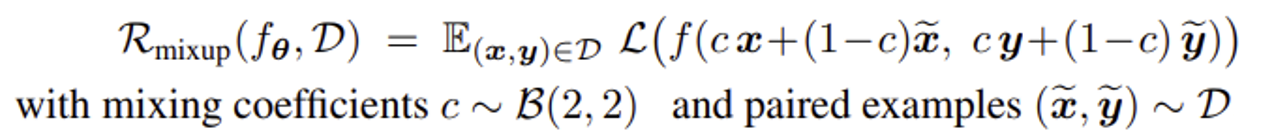
- $c$: 각 데이터 포인트가 혼합된 새로운 데이터에 기여하는 정도
- 각 iteration마다 새로운 $c$와 데이터 쌍을 샘플링해야 함
Selective mixup: 특정 조건인 $\text{Paired(} \cdot, \cdot)$가 true일 때만 두 데이터를 혼합함

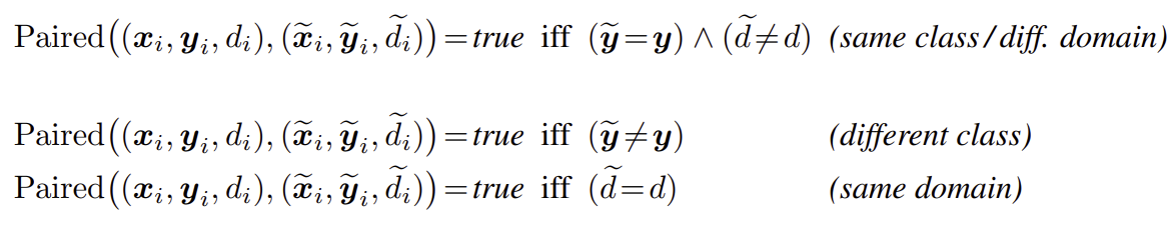
Theoretical Predictions: Selective Mixup Modifies the Training Distribution

Training distribution: $\mathcal{D}$에서 샘플링한 예시들의 분포 (mixup 여부와 상관 없음)
With ERM: training distribution은 $\mathcal{D}$의 $y$ 분포와 같음 ($p_Y(\mathcal{D}) = \oplus_{(x, y) \in \mathcal{D}} y / \vert D \vert$)
With selective mixup
- 데이터 쌍에서 첫 번째 데이터의 training distribution은 $\mathcal{D}$의 $y$ 분포와 같음 ($p_Y(\mathcal{D}) = \oplus_{(x, y) \in \mathcal{D}} y / \vert D \vert$)
- 데이터 쌍에서 두 번째 데이터는 어떤 조건을 사용하는지에 따라 training distribution이 다름
Regression toward the mean:
- 만약 두 번째 데이터가 첫 번째 데이터와 같은 class에서 뽑힌다면 $p_Y(\mathcal{\tilde{D}}) = p_Y (\mathcal{D})$임 (resampling 효과 없음)
- 만약 두 번째 데이터가 첫 번째 데이터와 다른 class나 다른 domain에서 뽑는다면 $p_Y(\mathcal{\tilde{D}}) = 1 - p_Y (\mathcal{D})$ (resampling 효과 있음)
When does one benefit from the resampling (regardless of mixup)?
- Resampling으로 인해 훈련 데이터의 분포가 테스트 데이터 분포에 더 가까워지기 때문에 훈련 데이터와 테스트 데이터 간의 분포 차이에 대응할 수 있음

Theorem 3.1.

Given a dataset $\mathcal{D} = {(x_i, y_i)}_i$ and paired data $\tilde{\mathcal{D}}$ sampled according to the “different class” criterion, i.e. $\tilde{\mathcal{D}} = {(\tilde{x}_i, \tilde{y}_i) \ \sim \ \mathcal{D} \ \ s.t. \ \ \tilde{y}_i \neq \tilde{y}_j}$, then the distribution of classes in $\mathcal{D} \ \cup \ \tilde{\mathcal{D}}$ is more uniform than in $\mathcal{D}$.

Formally, the entropy $\mathbb{H} (p_Y(\mathcal{D})) \leq \mathbb{H} (p_Y(\mathcal{D} \cup \tilde{\mathcal{D}}))$.

엔트로피는 분포가 얼마나 균등하게 퍼져 있는지 수치화한 것이다. 엔트로피 값이 높을수록 분포가 더 균일하다. 즉 불확실성이 높다.

Untitled

Empirical Verification

Waterbirds: 두 종류의 새와 두 종류의 배경이 있고, 두 종류의 새를 구별해야 한다. 그런데 훈련 데이터에서 특정 종류의 새가 주로 한 종류의 배경과 함께 나타나는 경향이 있다. 물새는 주로 물 배경과, 땅새는 주로 땅 배경과 함께 나타난다. 하지만 테스트 데이터에서는 이러한 상관관계가 반전된다. 만약 모델이 배경에만 의존하여 새를 구별한다면 테스트 데이터에서 낮은 성능을 보일 것이다. 여기서 domain은 배경이다.

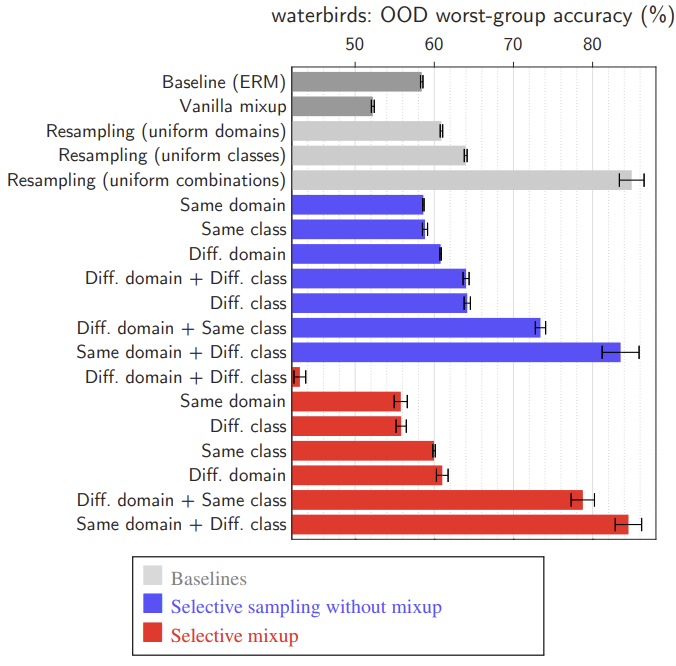
The excellent performance of the best version of selective mixup is entirely due to resampling.
CivilComments: 온라인 댓글이 toxic인지 아닌지 구별해야 한다. 각 데이터는 Christian, male, LGBT 등 주제 속성을 나타내는 레이블이 지정되어 있다. 마찬가지로 훈련 데이터에서 이러한 속성들은 실제 독성 레이블과 잘못된 상관관계를 가지고 있다. 이 속성들을 domain 레이블로 사용한다. 이 데이터셋에서 사용하는 메트릭은 worst-group accuracy이다. 이는 독성 레이블과 주제 속성의 모든 가능한 조합에 대해 모델이 얼마나 잘 수행하는지를 측정한다. 모든 가능한 조합 중 가장 정확도가 낮은 그룹을 찾아낸다.
Wild-Time Yearbook: 여자인지 남자인지 구별한다. 여기서 domain은 시간대이다.
Wild-Time arXiv: 논문을 172개의 class로 분류한다. 여기서 domain은 시간대이다.
Wild-Time MIMIC-Readmission: 이 데이터셋은 병원 기록을 포함하고 있다. 병원 기록을 바탕으로 환자가 병원에 재입원할지 여부를 분류하는 두 가지 class가 있다. 여기서 domain은 시간대이다.

paper

https://arxiv.org/abs/2305.16817