Semantic Uncertainty: Linguistic Invariances for Uncertainty Estimation in Natural Language Generation
ICLR 2023 notable top 25%
Introduction
자연어 생성(Natural Language Generation, NLG) 기술은 많이 발전했지만, 모델의 불확실성을 측정하는 방법에 대한 논의는 부족한 상황이다. 그러나 불확실성을 정확하게 측정하는 것은 더 안전한 AI 시스템을 구축하는 데 필수적이다.
자연어 생성(Natural Language Generation, NLG)에서 불확실성을 측정하는 과정은 다른 기계 학습 task와 다른 어려움이 존재한다. 다른 기계 학습 task는 상호 배타적인(mutually exclusive) 출력을 가진다. 예를 들어 분류 task를 할 때 ‘고양이’ class와 ‘강아지’ class는 완전히 다르다. 반면 NLG에서는 같은 의미를 지닌 다양한 출력을 생성할 수 있다. 예를 들어 “The capital of France is Paris”와 “France’s capital is Paris”는 동일한 의미를 가지는 두 가지 표현이다. 이러한 특성 때문에 NLG에서는 불확실성 측정이 더 복잡해진다.
NLG에서 불확실성을 측정하는 한 방법은 predictive entropy를 계산하는 것이 다. 이는 주어진 입력에 대해 출력이 가지는 정보량을 측정한다. 출력의 정보량이 적을수록 높은 entropy 값을 가지게 된다. Predictive entropy는 다음과 같이 계산된다.
\[PE(x) = H(Y \vert x) = -\int p(y \vert x) \log{p(y \vert x)} dy\]여기서 token 수준의 likelihood를 계산하게 되는데, 문제는 우리가 고려해야 할 것이 token 수준이 아니라 meaning 수준이라는 것이다. 따라서 token 수준의 likelihood가 아닌 semantic likelihood를 사용해야 한다. 예를 들어 “The capital of France is Paris”와 “France’s capital is Paris”는 meaning 수준에서 비슷한 likelihood를 가져야 한다. 그러나 token 수준에서 likelihood를 계산하면 두 문장이 같은 의미를 지니고 있는지 제대로 파악할 수 없다.
Uncertainty 측정
Step 1. Generation
- Predictive distribution을 기반으로 $M$개의 response를 생성한다.
-
Predictive distribution은 다음과 같이 계산한다.
\[\log p(s \vert x) = \sum_i \log p(s_i \vert s_{<i})\]
Step 2. Clustering by semantic equivalence
- 동일한 의미를 가지는 sequence끼리 clustering한다.
- 만약 sequence $s$와 sequence $s’$가 같은 의미를 가진다면, 이들의 관계를$E(s, s’)$로 나타낸다.
- $E(s, s’)$ 관계를 가지는 sequence 그룹을 $c$라고 하며, 이러한 $c$의 집합을 space of semantic equivalence classes $\mathcal{C}$라고 한다.
- Bi-directional entailment algorithm을 사용해서 두 sequence가 같은 의미를 가지는지 판단한다.
- 자연어 추론(NLI)은 두 문장 관계를 분석하여 그 관계가 entailment, neutral, contradiction 중 어떤 것인지를 결정한다.
- 두 sequence 사이의 양방향 관계를 고려해서 두 방향 모두에서 entailment 결과를 보인다면 두 sequence는 같은 의미를 가진다고 판단한다.
Step 3. Computing the semantic entropy
- Token 수준의 likelihood가 아닌 meaning 수준의 likelihood을 계산한다.
- Token 수준의 likelihood: $p(s \vert x) = \prod_i p(s_i \vert s_{<i}, x)$
- Meaning 수준의 likelihood: $p(c \vert x) = \sum_{s \in c} p(s \vert x) = \sum_{s \in c} \prod_i p(s_i \vert s_{<i}, x)$
- 앞서 계산한 likelihood를 기반으로 semantic entropy를 계산한다.
- $SE(X) = -\sum_c p(c \vert x) \log p(c \vert x)$
Example
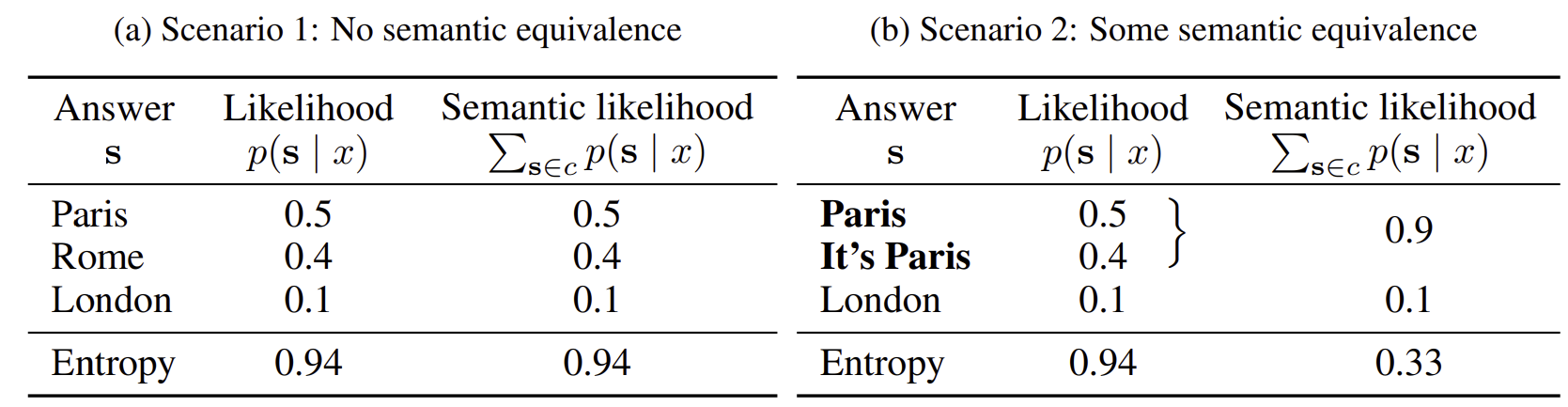
“What is the capital of France?”에 대한 답변을 두 경우로 나누어서 entropy를 계산해보았다. (a)의 경우에는 생성된 모든 답변이 서로 다른 의미를 가진다. 따라서 token 수준의 likelihood와 meaning 수준의 likelihood를 기반으로 계산한 entropy 값이 같다. 하지만 (b)의 경우에는 생성된 답변 중 일부가 같은 의미를 가진다. Semantic likelihood에서는 두 답변이 같은 의미를 가질 경우 그 둘의 likelihood를 더한다. 따라서 token 수준의 likelihood로 계산했을 때와 meaning 수준 likelihood로 계산했을 때 entropy 값이 다르다. Meaning 수준 likelihood로 계산한 entropy를 semantic entropy라고 부른다. (b)의 경우 entropy가 더 낮아야 하는데 semantic entropy는 이를 잘 반영하고 있다.
Results
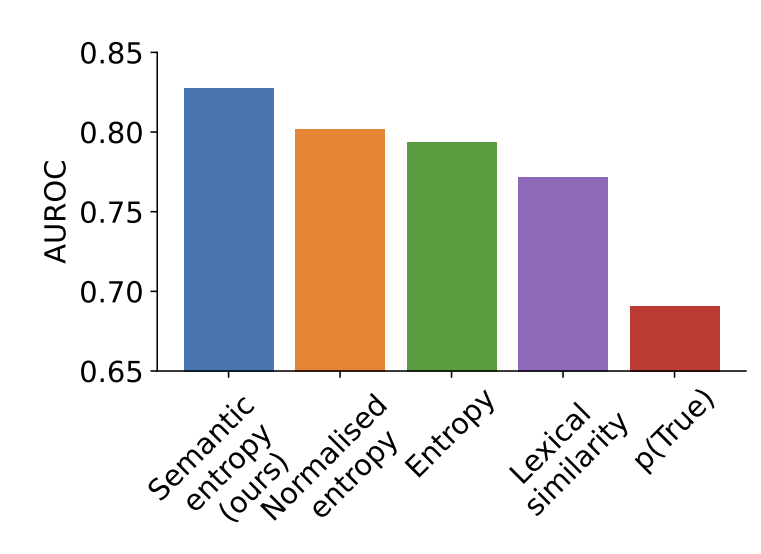
실험에 사용한 데이터셋은 question answering task에 관한 TriviaQA 데이터셋이다. Metric으로는 AUROC를 사용했다. AUROC는 false positive rate을 가로축으로, true positive rate을 세로축으로 하는 ROC 곡선 아래의 면적이다. Semantic entropy을 사용했을 때 다른 baseline보다 AUROC 값이 높다. 즉 semantic entropy가 다른 baseline보다 모델 accuracy를 더 잘 예측한다.
paper